In this post, I’d like to talk about Comma-Separated Values in Files (i.e. CSV Files).
I had a client with a need to read in a CSV file and do some subsequent processing with it. This was a very small file that didn’t regularly populate any permanent table… Its data was simply used as input to do some calculations, so using a tool like SSIS to process the file was overkill. We just needed to access the file directly with T-SQL.
Let’s look at an example…
In the C:\Temp folder, we have a CSV File called TerritoryData.CSV with the following contents (Ignore the /*…*/ delimiters… They are there so that sites that syndicate this blog will render the output more reliably):
/*
TerritoryID,TotalSales,TotalCost
1,5767341.98,4746522.45
2,3857163.63,3174445.67
3,4677108.27,3849260.11
4,8351296.74,6873117.22
5,2851419.04,2346717.87
6,6917270.88,5692913.94
7,3899045.69,3208914.61
8,2481039.18,2041895.24
9,1977474.81,1627461.77
10,3514865.91,2892734.64
*/
One method we can use to directly access a CSV file using T-SQL (and the one most recommended on various online forums) is to do something like this:select TerritoryID ,TotalSales ,TotalCostfrom openrowset('MSDASQL' ,'Driver={Microsoft Access Text Driver (*.txt, *.csv)}' ,'select * from C:\Temp\TerritoryData.CSV')/* TerritoryID TotalSales TotalCost ----------- ----------- ----------- 1 5767341.98 4746522.45 2 3857163.63 3174445.67 3 4677108.27 3849260.11 4 8351296.74 6873117.22 5 2851419.04 2346717.87 6 6917270.88 5692913.94 7 3899045.69 3208914.61 8 2481039.18 2041895.24 9 1977474.81 1627461.77 10 3514865.91 2892734.64 */This uses the MSDASQL provider in concert with the Microsoft Access Text Driver to read the data from the CSV File.
Boy that was easy! We’re done, right?
Well… not really. There are some inherent gotchas and problems with this.
First of all, this approach with OPENROWSET will not work unless your server is configured to accept Ad Hoc Distributed Queries. That can easily be accomplished like so:
sp_configure 'Ad Hoc Distributed Queries',1reconfigureNote the name of the Driver in the query. My laptop has the Microsoft Access Text Driver installed on it… presumably because I’m on Windows 7 and Office 2010 is the only version of Office that I have installed (and, ironically, I did NOT choose to install Access). But on my old WinXP machine, there is no such driver. On that machine, I would have to use a different driver name:
select TerritoryID ,TotalSales ,TotalCostfrom openrowset('MSDASQL' ,'Driver={Microsoft Text Driver (*.txt; *.csv)}' ,'select * from C:\Temp\TerritoryData.CSV')By the way, note the subtle difference in that the older driver separates *.txt and *.csv with a semicolon; whereas, the newer (Access) driver separates them with a comma. You have to make sure the driver is spelled EXACTLY right.
So, in a nutshell, we have to know which driver is installed in order to make this work. To see the drivers installed in your system, go to Control Panel -> Administrative Tools -> Data Sources (ODBC) -> Drivers.
Note that our CSV file was in the C:\Temp folder. This path has to be visible to the server. In my case, on my laptop, it’s not a problem… my server is my machine. But if the server is on another machine somewhere out there on the network or in the cloud, then C:\Temp does not refer to a path on my local machine running SSMS, but to a path on that machine on which the server is installed. This is not a big problem, but it is something that you have to be aware of.
But the name of that path can be a problem. Let’s say instead of putting the CSV file in the C:\Temp folder, we decide to put it into a folder called C:\CSV Files. If we try to execute that, here’s what happens:
select TerritoryID ,TotalSales ,TotalCostfrom openrowset('MSDASQL' ,'Driver={Microsoft Access Text Driver (*.txt, *.csv)}' ,'select * from C:\CSV Files\TerritoryData.CSV')/* OLE DB provider "MSDASQL" for linked server "(null)" returned message "[Microsoft][ODBC Text Driver] Syntax error in FROM clause.". Msg 7321, Level 16, State 2, Line 2 An error occurred while preparing the query "select * from C:\CSV Files\TerritoryData.CSV" for execution against OLE DB provider "MSDASQL" for linked server "(null)". */It’s that darn space character embedded in the folder name that causes the problem. Even if we put double-quotes around the path and filename, it still doesn’t work, displaying a different error message:
select TerritoryID ,TotalSales ,TotalCostfrom openrowset('MSDASQL' ,'Driver={Microsoft Access Text Driver (*.txt, *.csv)}' ,'select * from "C:\CSV Files\TerritoryData.CSV"')/* OLE DB provider "MSDASQL" for linked server "(null)" returned message "[Microsoft][ODBC Text Driver] The Microsoft Access database engine could not find the object 'C:\CSV Files\TerritoryData.CSV'. Make sure the object exists and that you spell its name and the path name correctly. If 'C:\CSV Files\TerritoryData.CSV' is not a local object, check your network connection or contact the server administrator.". Msg 7350, Level 16, State 2, Line 1 Cannot get the column information from OLE DB provider "MSDASQL" for linked server "(null)". */Luckily this problem can be overcome by removing the path from the filename and specifying it as the DefaultDir in the Provider String parameter (the second parameter) of OPENROWSET:
select TerritoryID ,TotalSales ,TotalCostfrom openrowset('MSDASQL' ,'Driver={Microsoft Access Text Driver (*.txt, *.csv)}; DefaultDir=C:\CSV Files\' ,'select * from TerritoryData.CSV')/* TerritoryID TotalSales TotalCost ----------- ----------- ----------- 1 5767341.98 4746522.45 2 3857163.63 3174445.67 3 4677108.27 3849260.11 4 8351296.74 6873117.22 5 2851419.04 2346717.87 6 6917270.88 5692913.94 7 3899045.69 3208914.61 8 2481039.18 2041895.24 9 1977474.81 1627461.77 10 3514865.91 2892734.64 */What if the filename itself has a space in it? If we rename the file to Territory Data.CSV, then we have a problem again:
select TerritoryID ,TotalSales ,TotalCostfrom openrowset('MSDASQL' ,'Driver={Microsoft Access Text Driver (*.txt, *.csv)}; DefaultDir=C:\CSV Files\' ,'select * from Territory Data.CSV')/* OLE DB provider "MSDASQL" for linked server "(null)" returned message "[Microsoft][ODBC Text Driver] Syntax error in FROM clause.". Msg 7321, Level 16, State 2, Line 1 An error occurred while preparing the query "select * from Territory Data.CSV" for execution against OLE DB provider "MSDASQL" for linked server "(null)". */But this problem can be fixed by putting double quotes around the filename:
select TerritoryID ,TotalSales ,TotalCostfrom openrowset('MSDASQL' ,'Driver={Microsoft Access Text Driver (*.txt, *.csv)}; DefaultDir=C:\CSV Files\' ,'select * from "Territory Data.CSV"')/* TerritoryID TotalSales TotalCost ----------- ----------- ----------- 1 5767341.98 4746522.45 2 3857163.63 3174445.67 3 4677108.27 3849260.11 4 8351296.74 6873117.22 5 2851419.04 2346717.87 6 6917270.88 5692913.94 7 3899045.69 3208914.61 8 2481039.18 2041895.24 9 1977474.81 1627461.77 10 3514865.91 2892734.64 */By the way, you may have noticed that the TerritoryID output above is right-justified in the output, indicating that the Text Driver made a “best guess” (based on the data it saw in the column) that the column was numeric. Sometimes you don’t want the Text Driver to assume anything about the column datatypes. For example, if you are importing a CSV file that has Zip Codes or Social Security Numbers, for example, you want those imported as character data, but the Text Driver will only see digits in its sampling and will insist on making it numeric data (thereby losing leading zeroes). You can get around this by creating a SCHEMA.INI file to describe the contents of your CSV files. You can read more about that here.
Another problem with this OPENROWSET(‘MSDASQL’) approach is that it assumes the MSDASQL provider is installed. I naïvely thought that this was installed by default when SQL Server is installed. Apparently it’s not. And unfortunately, my client did NOT have this in his list of providers. To see which providers you have installed, go to the Object Explorer in SSMS and look under Server Objects -> Linked Servers -> Providers:
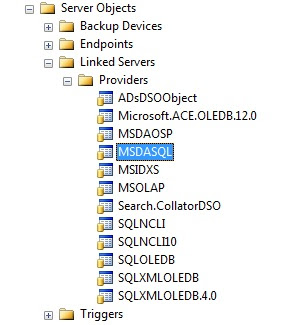
Finally, the OPENROWSET command expects only string literals for its parameters, so you cannot attempt to use variables like so:
declare @FilePath varchar(100) = 'C:\CSV Files\' ,@FileName varchar(100) = 'Territory Data.CSV'select TerritoryID ,TotalSales ,TotalCostfrom openrowset('MSDASQL' ,'Driver={Microsoft Access Text Driver (*.txt, *.csv)}; DefaultDir='+@FilePath ,'select * from "'+@FileName+'"')/* Msg 102, Level 15, State 1, Line 8 Incorrect syntax near '+'. */So, if you have the Path and Filename in variables, the only way you can accomplish reading in that file’s data is via Dynamic SQL, like so:
declare @FilePath varchar(100) = 'C:\CSV Files\' ,@FileName varchar(100) = 'Territory Data.CSV' ,@SqlStmt nvarchar(max) set @SqlStmt=N' select TerritoryID ,TotalSales ,TotalCost from openrowset(''MSDASQL'' ,''Driver={Microsoft Access Text Driver (*.txt, *.csv)}; DefaultDir='+@FilePath+N''' ,''select * from "'+@FileName+N'"'')' exec sp_executesql @SqlStmt/* TerritoryID TotalSales TotalCost ----------- ----------- ----------- 1 5767341.98 4746522.45 2 3857163.63 3174445.67 3 4677108.27 3849260.11 4 8351296.74 6873117.22 5 2851419.04 2346717.87 6 6917270.88 5692913.94 7 3899045.69 3208914.61 8 2481039.18 2041895.24 9 1977474.81 1627461.77 10 3514865.91 2892734.64 */So, to recap, if you want to use the OPENROWSET(‘MSDASQL’) approach, use the following guidelines:
- The server must be configured to allow Ad Hoc Distributed Queries
- The MSDASQL Provider must be installed on the server
- Reference the correct Text Driver name in the Provider String parameter
- Make sure the file path is visible to the server
- Specify the file path in the DefaultDir of the Provider String parameter
- Surround the filename with double-quotes in the query parameter of OPENROWSET
- Use a SCHEMA.INI file if you want more control over the datatypes of the columns
- Either hard-code the path and filename or use Dynamic SQL if the path and filename are in variables
Since my client didn’t have the MSDASQL provider at all, I had to come up with a completely different approach to reading in the CSV file.
One approach is to use OPENROWSET(BULK) instead. If we create a complex XML format file that describes our CSV File contents like so (without the /* … */ of course)…
/*
<?xml version="1.0"?>
<BCPFORMAT xmlns="http://schemas.microsoft.com/sqlserver/2004/bulkload/format"
xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance">
<RECORD>
<FIELD ID="1" xsi:type="CharTerm" TERMINATOR="," MAX_LENGTH="10"/>
<FIELD ID="2" xsi:type="CharTerm" TERMINATOR="," MAX_LENGTH="20"/>
<FIELD ID="3" xsi:type="CharTerm" TERMINATOR="\r\n" MAX_LENGTH="20"/>
</RECORD>
<ROW>
<COLUMN SOURCE="1" NAME="TerritoryID" xsi:type="SQLINT"/>
<COLUMN SOURCE="2" NAME="TotalSales" xsi:type="SQLDECIMAL"/>
<COLUMN SOURCE="3" NAME="TotalCost" xsi:type="SQLDECIMAL"/>
</ROW>
</BCPFORMAT>
*/
…then we can reference that format file as a parameter in a call to OPENROWSET(BULK):select TerritoryID ,TotalSales ,TotalCostfrom openrowset(bulk 'C:\CSV Files\Territory Data.CSV' ,formatfile='C:\CSV Files\Territory Data.FMT' ,firstrow=2) CSVInput/* TerritoryID TotalSales TotalCost ----------- ----------- ----------- 1 5767341.98 4746522.45 2 3857163.63 3174445.67 3 4677108.27 3849260.11 4 8351296.74 6873117.22 5 2851419.04 2346717.87 6 6917270.88 5692913.94 7 3899045.69 3208914.61 8 2481039.18 2041895.24 9 1977474.81 1627461.77 10 3514865.91 2892734.64 */Note that we had to specify FIRSTROW=2 to skip over the header row in the CSV file that had the column names.
This approach works fine, but it’s kind of a pain to have to set up the format file. For any new CSV File that we wanted to process, we would have to create one of these format files. No thanks.
Another approach… much easier… is to use BULK INSERT, like so:
if object_id('tempdb..#TerrData','U') is not null drop table #TerrDatacreate table #TerrData ( TerritoryID int ,TotalSales decimal(12,2) ,TotalCost decimal(12,2) ) bulk insert #TerrData from 'C:\CSV Files\Territory Data.CSV'with (fieldterminator=',' ,rowterminator='\n' ,firstrow=2) select * from #TerrData/* TerritoryID TotalSales TotalCost ----------- ----------- ----------- 1 5767341.98 4746522.45 2 3857163.63 3174445.67 3 4677108.27 3849260.11 4 8351296.74 6873117.22 5 2851419.04 2346717.87 6 6917270.88 5692913.94 7 3899045.69 3208914.61 8 2481039.18 2041895.24 9 1977474.81 1627461.77 10 3514865.91 2892734.64 */It can’t get much more simple than that!
But, of course, there’s a catch…
The BULK INSERT and the OPENROWSET(BULK) approaches simply won’t work in certain cases. Let’s say we had data in Excel that looked like this:
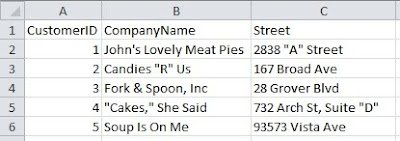
If we save that as a CSV file, its contents would look like this (without the /* … */):
/*
CustomerID,CompanyName,Street
1,John's Lovely Meat Pies,"2838 ""A"" Street"
2,"Candies ""R"" Us",167 Broad Ave
3,"Fork & Spoon, Inc",28 Grover Blvd
4,"""Cakes,"" She Said","732 Arch St, Suite ""D"""
5,Soup Is On Me,93573 Vista Ave
*/
You can see that any string column that contained a double-quote character or a comma is surrounded (or delimited) with double-quote characters… and the embedded double-quote characters are doubled up.If we try to read that in, we certainly don’t get what we want:
if object_id('tempdb..#CustData','U') is not null drop table #CustDatacreate table #CustData ( CustomerID int ,CompanyName varchar(40) ,Street varchar(40) ) bulk insert #CustData from 'C:\CSV Files\Customer Data.CSV'with (fieldterminator=',' ,rowterminator='\n' ,firstrow=2) select * from #CustData/* CustomerID CompanyName Street ---------- ----------------------- --------------------------------------- 1 John's Lovely Meat Pies "2838 ""A"" Street" 2 "Candies ""R"" Us" 167 Broad Ave 3 "Fork & Spoon Inc",28 Grover Blvd 4 """Cakes "" She Said","732 Arch St, Suite ""D""" 5 Soup Is On Me 93573 Vista Ave */We get the surrounding double-quotes and the embedded double double-quotes as part of our data… and the commas within our string columns are interpreted as being column separators.
Yuk!
I guess this is why tab-delimited files were invented. But, interestingly enough, Excel insists on doing the same double-quote delimiting when you save data as a tab-delimited file as well.
So what now?
I was stubborn. I wasn’t going to let these limitations stand in my way. I was determined to come up with a fairly generic way of handling a CSV file in T-SQL.
So I wrote a procedure called usp_ProcessCSVFile. It accepts the (fully-qualified) name of a CSV File, appropriately handling the double-quote delimiters (and the embedded commas and double double-quotes) in the data, and it produces rows containing columns of datatype VARCHAR(100). We can just INSERT the procedure results into a destination table and the columns will be converted appropriately.
For example…
if object_id('tempdb..#CustData','U') is not null drop table #CustDatacreate table #CustData ( CustomerID int ,CompanyName varchar(40) ,Street varchar(40) ) insert #CustData exec usp_ProcessCSVFile 'C:\CSV Files\Customer Data.CSV' select * from #CustData/* CustomerID CompanyName Street ---------- ----------------------- ---------------------- 1 John's Lovely Meat Pies 2838 "A" Street 2 Candies "R" Us 167 Broad Ave 3 Fork & Spoon, Inc 28 Grover Blvd 4 "Cakes," She Said 732 Arch St, Suite "D" 5 Soup Is On Me 93573 Vista Ave */The procedure also accepts an optional second parameter (@HeaderRowExists), a bit column that defaults to 1. If your CSV file does not contain a header row, then pass a 0 for this parameter and it will process the first row as actual data instead of a header row.
I would have liked to create a function rather than a procedure to process CSV Files, but that was impossible because I had to use Dynamic SQL in order to handle the filename being in a variable/parameter, because I’m using OPENROWSET(BULK), which, as I mentioned earlier, only accepts string literals.
In short, the procedure reads the contents of the CSV File (using OPENROWSET(BULK)) into a single VARCHAR(MAX) variable called @CSVContents, and then it converts it from comma-separated data into tab-separated data, at the same time taking care of any special string columns that contain double-quotes or commas. It then inserts XML tags (<row></row> and <col></col>) into @CSVContents to designate the rows and columns and then, finally, it CASTs @CSVContents into XML and shreds it… something like this (for a 3-column CSV File):
select [Column1]=XMLNode.value('(col[1]/text())[1]','varchar(100)') ,[Column2]=XMLNode.value('(col[2]/text())[1]','varchar(100)') ,[Column3]=XMLNode.value('(col[3]/text())[1]','varchar(100)')from (select XMLData=cast(@CSVContents as xml).query('.')) F_XMLcross apply XMLData.nodes('/row') F_Node(XMLNode)There were a few challenges in making this work, but you can see how I accomplished it in the comments of the code, which you can download from my SkyDrive.
Considering that the procedure is potentially doing a lot of string manipulation (with a VARCHAR(MAX) variable), the performance is certainly not stellar, since T-SQL is not known for its rapid string processing prowess. The larger the file, and (especially) the more double-quote delimiters you have in the file, the longer it will take. To process a CSV file of 50,000 rows and 4 columns (3MB in size) that contained no double-quote delimiters at all (and INSERTing the data into a temp table) takes a little over 20 seconds on my laptop. Again, that’s frightfully slow, but if you need to process that much data, you should probably be using SSIS instead. This procedure is primarily designed for relatively small quick files that BULK INSERT will not handle correctly.
I hope you find this utility to be useful. I certainly had fun writing it.
UPDATE Feb2017: A newer faster version of this stored procedure has been posted to my Google Drive.




